The mtof object can take a MIDI note number and output the frequency of that note in standard 12-tone equal temperament tuning (aka 12-EDO). But what if you want to get away from this musical dogma? How about we start to explore say 13-EDO, 7-EDO, 24-EDO, or 41-EDO with Max/MSP?
Equal temperament on Wikipedia
Equal temperament on the Xenharmonic Wiki
Some years ago I wrote an expression that could quickly be dropped into any Max/MSP synth and then play microtonal equal temperaments. It’s a more generalised version of mtof and I want to share that with you today. It’s an mtof-killer!
First let’s take a quick look inside the mtof object and see how it works. Really, mtof just performs one simple expression.
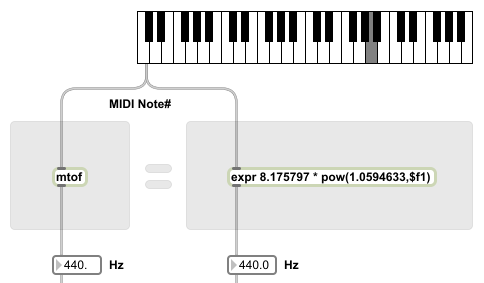
Here is my mtof-killer expression in all its beasthood:
Nasty, right?
Copy and paste this code into Max/MSP and continue along with this tutorial.
----------begin_max5_patcher---------- 882.3ocyXE0aaBCD94To9evh0GZlxRwfwD1aapaR8gsIsWampHfSp6.Cy3zl 1p0e6yXGRnYg.AkRSdvN9riuu6ymu6bd53i5YLNYNIy.7Qvkfd8dRJomRVtj dEB5YD6OOHxOSsPCF49jw2ZLXwbBxbgRtfSedozjYhHhP7PJQu4FYzoL+HCv uJVwjDlf4Gql23SbpbxhongJgRs7AK7RorYwTlbSUnvtPZpuH3FJa50bRfPq KanyPyA.aSq7NDNu0xbn4JcK2JM.U6ErLjxnOpfDT9iUh+6wGk2K6FzXJZpO kUOWL.XPYhRTRY6FsY61pA1sMJuCpGYgp1vKsYb4Igfvulv7GGovY6sdxig9 AOuwSSq1aUiTmiHmh1pLp1i6IQIxsp5iM479h7Ssw9ro6tmLby1Nrda2xEl2 4XVmm71OP26t4RkOlvqlvx8t+e5RZ6zXIOuNjpmBg0QgRzUr0PK2sPrXOUrA 3H6WShckbdruRynCTmSuc22zAiGZK+3hd04wCTRyc2IMDxbHV9wBujzrcOvH semEQCav05Wl6JkSxHLguflvJYvJOBScZIU.bG6xFZI1zo0oFbvUt+cR9tfj 3XRNmrdEQ+jLgvIr.B3aWb9EfumHHua4phnLRPxLl3EHaBe5XEZFtkXifOmD EtIOR6Z7HyQ1syxDzIz.0IUc9qXWOUbRzn7N8.6sTQw92arAj6W4j+LS9sGd U4Vq8M253fVE.8.jf+x4+vX+PcsnxGjq6tGnrCImN5B8nQsnnQKUfPnKZnir T42.WppdgHYdJGb5ISrAmARStGbpt05pqFHKv8rSlX0W90Snn98Aueqq.1u5 zSaMOdkLMthXmnFTdNTUdts2avKMS8YjUEmLdZPRTBe8TuEMdlPO7FS9Bwsv OyT+NS88RDVwEPSul+zL85TWbV++fPou7IVy3yRlwCJNoKdnLnjFCIxPvrkA fub0COKupanggD1K79CoY4kBDVSs.MFX4NTM.XvNGX6.iA2JvhogoIxp.yJh 6nB3X6piVKeLPwnR5ZeaK3FYKntmjgMBX3NGXvFALkyqcmBLuFiKqNEWtMFW vNEWNMFWls3VLbQNsRiZ1s3Ewz8SSuivyVfFsUHybcqN4DdfdLkoGqSyXvI2 QK9I5+fWCetLsiPlyYFWmEe9HrgbFkBkM+yHSxvn -----------end_max5_patcher-----------
The ‘EDO’ value sets what equal tempered tuning you want. So a setting of 5 gives you 5-EDO, a setting of 34 gives you 34-EDO.
‘Reference Frequency’ is the standard pitch for the scale. Usually in Western music A = 440 Hz. You can also use 432 Hz if you believe in crystal healing and reptilian world leaders.
‘Reference MIDI Note#’ is the MIDI note to be tuned to the reference frequency (above). This could be MIDI note 69 if you want to tune to middle A, or MIDI note 60 if you want to tune to middle C.
For starters, try 5 for the EDO value, 440 Hz for the reference frequency and 69 for the reference MIDI note number. Have a play on the keyboard. It’s a cool sounding pentatonic scale, right?
If you played with my example patch and got it working, then you don’t need to read this section. Just start using it in your projects and have fun exploring equal temperaments.
But if you absolutely must know how this magic is done, then keep reading! (Warning: I will assume that you already understand how to make expressions with the expr object).
Let’s look back at the original mtof expression, try to understand it, and then try to generalise it.
Output frequency = 8.175797 * pow(1.0594633,$f1)
Note that pow(a,b) is just the expr object’s way of saying a^b.
8.175797 is the frequency (in Hz) for MIDI note 0.
$f1 is the MIDI note number being played.
1.0594633 is the size of the smallest step size in 12-EDO. It is the value of a semitone.
Therefore an mtof object has this general structure:
Output frequency = Frequency of MIDI note 0 * pow(step size,MIDI note number)
Let’s start by swapping the step size of 1.0594633 with the step size from any n-EDO we want. But how do we calculate the step size? For n-EDO, it’s calculated like this:
step size of n-EDO = pow(2,1.0/n)
So let’s bring that into our in-progress generalised mtof:
Output frequency = Frequency of MIDI note 0 * pow( pow(2,1.0/n),MIDI note number )
That’s great, but unless you want MIDI note 0 to always be equal to 8.175797 Hz, how will we go about tuning our scale up to some standard pitch? Well first we need to know what our standard pitch is (aka reference frequency) and we also need to know what MIDI note number to assign that reference frequency to. Once we know these, we work backwards to find the frequency at MIDI note 0.
If our reference MIDI note number is higher than 0, then the frequency at MIDI note 0 will always be lower than the frequency at the reference MIDI note number. In fact:
Frequency at MIDI note 0 = reference frequency / pow(step size,reference MIDI note number)
We can re-use the step size calculation from before and insert it into the above calculation for MIDI note 0 frequency:
Frequency at MIDI note 0 = reference frequency / pow( pow(2,1.0/n),reference MIDI note number )
Above, we’ve just found a way to calculate the frequency at MIDI note 0 for any reference frequency assigned to any MIDI note number for any EDO of size n. That’s the entire left side of the mtof-killer worked out. So let’s bring alllll of this together:
Output frequency = Frequency of MIDI note 0 * pow(step size,MIDI note number)
= (reference frequency / pow( pow(2,1.0/n),reference MIDI note number )) * pow( pow(2,1.0/n),MIDI note number )And finally we replace these English-language variables with integers and floats in expr format, such that:
$i1 = MIDI note number from the keyboard
$f2 = n-EDO
$f3 = reference frequency
$f4 = reference MIDI number
($f3 / pow ( pow (2,1.0/$f2),$i4)) * pow ( pow (2,1.0/$f2),$i1)
Well done if you kept up! I hope that explains how this expression alone can allow you to play microtonal equal tempered tunings in your Max/MSP projects.
UPDATE: Homebrewed methods like my one above are often inefficient. A commenter Toby noted:
This does the same thing in a simpler way:
expr $f3 * pow(2,($f1-$f4)/$f2)
If you need more power than this, for example you wish to create scales with arbitrary and variable step sizes, or you wish to play just intonation scales, then you should read How to play microtonal scales on a Max/MSP synth.

Thanks for listening.
This does the same thing in a simpler way:
expr $f3 * pow(2,($f1-$f4)/$f2)
I’m gonna try this when I get home. Thanks!
How would you do the same thing if you had 3 different step sizes, where step size 1 appears 7 times, step size 2 appears 5 times and step size 3 appears 10 times?
In this case the expr object won’t help – try using the coll method instead:
https://sevish.com/2014/how-to-play-microtonal-scales-on-a-maxmsp-synth/
It involves specifying your scale using with Scala or Scale Workshop, exporting as a txt file (Max/MSP coll format) and then load that into the coll object.
Would it be possible to use 3 different expressions and allocate specific notes to specific expressions using a switch of gate system?
I know coll is an option, I’ve looked into it but I’m trying to figure out if this is possible.
Would it be possible to use 3 different expressions and allocate specific notes to specific expressions using a switch or gate system?
I know coll is an option, I’ve looked into it but I’m trying to figure out if this is possible.